Overview
Order of growth of an algorithm is a way of predicting how long is the execution time of a program and the space/memory is required when the input size changes. We can have multiple solutions and need to determine the most efficient one to use.
For this purpose: we need to figure out which solutions are more efficient by identifying the time taken by all the solutions that are implemented, we write a polynomial (the worst case scenario) and then we see the order of growth of every time taken and which one has the least order of growth.
When we identify that the solution which has the least order of growth then we can say this algorithm is efficient.
The function can have:
- Least order of growth and
- Higher order of growth
A function f(n) is said to be growing faster i.e. higher order than g(n) if:
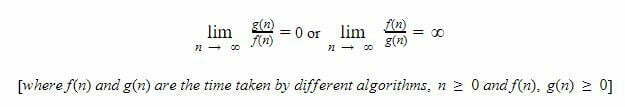
So if f(n) is growing faster i.e. having more order of growth then the algorithm whose time taken is represented by a function f(n) is a bad algorithm. This means an algorithm represented by function g(n) is better because it’s growing slower in terms of input size.
For example:
A function is f(n) is said to be growing faster than g(n) if: ![]()
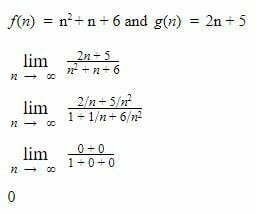
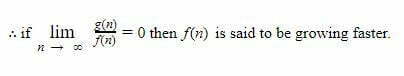
Easiest way to find and compare growths:
- Ignore lower order terms
- Ignore leading term constant
For example:
f(n) =2n2 + n + 6, order of growth: n2 (quadratic)
g(n) = 200n + 5, order of growth: n (linear)
Now if there is multiple terms and conditions then how we decide which one is leading, which one is not leading, which one is growing slower for that we can always use the basic mathematics terms like:
c < loglogn < logn < n1/3 < n1/2 < n < n2 < n3 < n4 < 2n < nn
That means: c grow very slowly, then loglogn and so on.
Following is the some exercise:
First,
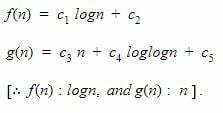
Since, the order of growth of g(n) is higher than f(n) hence g(n) is considered a bad algorithm.
Second,
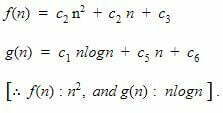
Since, the order of growth of f(n) is higher than g(n). Hence, f(n) is considered a bad algorithm.
Conclusion
In this post, we learn how we can determine the order of growth of a function so that we can analyze the best, average and worst case scenario during the analysis of an algorithm..